研究Studies

ファジィ測度

ファジィ測度とは、菅野が1972年の論文「Fuzzy測度とFuzzy積分」[2]において提案した、ルベーグ測度（確率測度）の拡張概念である[8]。（この概念を学術会議で初めて発表したのは、前年の「Fuzzy積分について」[1]である。）

【定義】
集合 X の部分集合 F に対して定義された集合関数で、つぎの性質をもつものをファジィ測度という。

ファジィ集合では、あいまいな容れ物 A と明確な要素 x があるときの「x ∈ A」のファジィネスを扱っているのに対し、明確な集合 B とよく分からない要素 y があるときの「y ∈ B」のファジィネスを扱うのがファジィ測度である[9]。 たとえば目の前に古い壺があったとき、「この壺は古い」という言明の意味のあいまいさがファジィ集合のファジィネスであり、「この壺は300年前から400年前のものである」という判断のあいまいさがファジィ測度のファジィネスである[10]。
ファジィ測度はものを測る主観的尺度として広く解釈されている [9]。

数学における一般的な「測度」は加法性をもつが、ファジィ測度は加法性をもたず単調性だけをもつという特徴がある。
非加法性によって部分集合間の相互作用を表すことができるので、ファジィ測度は、構成要素間に相互作用のあるシステムの記述に利用されている。 g(X) = 1 であるファジィ測度 g は、主観的な確からしさを表すのに用いられ、意思決定論などでは非加法的主観確率 (non-additive subjective probability) とも呼ばれる[11]。

ファジィ測度は単調性だけをもつため極めて一般的な集合関数といえるが、一方で、一般的すぎて数学的に理論展開しにくいという面をもつ。そこで、単調性よりも強い条件を仮定するファジィ測度の特殊型がいくつか提案されている[12]。
菅野の提案した「λ-ファジィ測度」[3] も特殊型である。

【定義】
次の性質をもつ\(\ \large{g}_{\small{\lambda}}\ \)を λ-ファジィ測度 と呼ぶ。

λ はパラメータであり、λ= 0 のとき、\(\ \large{g}_{\small{\lambda}}\ \)は確率測度になる[12]。

このほかの特殊型としては、
・Zadehによる「可能性測度」[17]
・Duboisらによる「必然性測度」[18][19]
・Weberによる「分解可能測度」[20]
・Shaferによる「belief関数」「plausibility関数」[21]
などが知られている。

ファジィ測度は、測度としての確率を拡張したものである。ファジィ測度は判断における不確かさを、さらにいくつかの様相に分けて表すスケールとして興味深いものである。そもそも可能性 (possibility)、必然性 (necessity あるいは certainty) というのは、カントが考えた様相である。たとえば、様相論理というのはカントの様相の考えに基づいて、命題の可能的、あるいは必然的な有様を議論するものである。
　ファジィ測度論は測度の解釈として様相概念を導入したものであり、そこでは確率は蓋然性測度として考えられている。可能性、必然性、蓋然性という判断の三つの様相が出てきたが、ある事象の生起の判断において、これらを度合の大きさの順に並べると、可能性＞蓋然性＞必然性 となる。たとえば、コインを投げて表がでる可能性は１、蓋然性は２分の１、必然性は０である。このことから、「確からしさ」という観点からは、可能性よりも蓋然性の方が確実性が大きいということになる[13]。

参考文献

ファジィ積分

菅野は1972年のファジィ測度の提案と同時に、ファジィ測度による積分概念を提案した[2]。今日、菅野積分と呼ばれている。この概念は、のちの博士論文「Theory of fuzzy integrals and its applications」[4]において、より体系的に論じられた。

【定義】
集合 X の部分集合 F 上の関数を\(\ h:F \rightarrow [0,1] \ \)、ファジィ測度を g とすると、h の g によるファジィ積分は次のように定義される。

菅野積分は任意のファジィ測度に対して定義されるが、特に可能性測度 π に適した積分であるといわれている[8]。
ファジィ測度がルベーグ測度の拡張であるのに対し、菅野積分はルベーグ積分の拡張ではない。しかし、計算が単純であり、その割には良い性質をもっているので、応用も数多く[14] 、多属性をもつ対象の主観的評価モデルとしてよく用いられている[9]。

また、2000年以降は、多基準意思決定モデルとしての菅野積分の拡張概念や、序数モデルにおける統合演算子としての菅野積分の研究が活発になってきている[16]。
例えば
・Grabischによる対称菅野積分[22]
・Grabischらによる累積プロスペクト理論(CPT)型菅野積分[23]
・Grabischらによる双容量に関する菅野積分[23]
・菅野による階層型菅野積分[7]
・Marichalによる束の値をとる菅野積分[24]
などがある。

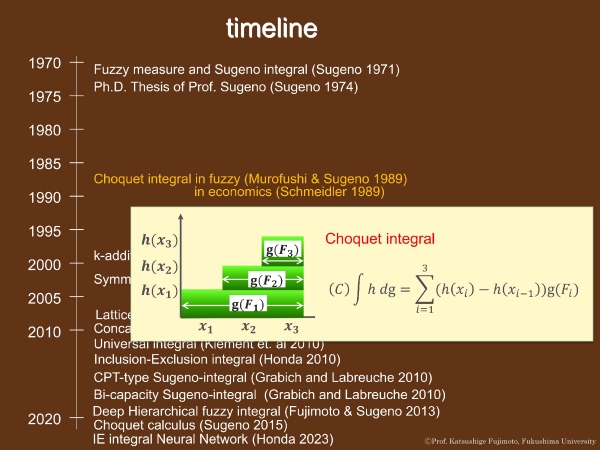
室伏、菅野[6]は一般の測度の拡張としてファジィ測度をとらえ、その積分型を与えた。この積分はChoquetが容量（特殊なファジィ測度）に関して定義した汎関数と一致するので、Choquet積分と呼ばれる[12]。

【定義】
集合 X の部分集合 F 上のファジィ測度を g 、X 上の実数値関数を h とすると、つぎの形式の積分をショケ積分という。

ショケ積分はルベーグ積分の自然な拡張であり、例えば、通常の有限測度に関するショケ積分はルベーグ積分に一致する。

　ファジィ測度が一般的に加法性を持たないので、その積分であるショケ積分も一般に加法性を持たない。このためショケ積分は、構成要素間に相互作用のある対象に関する総合化の操作に用いられる。例えば多属性評価のモデルでは、属性の集合の重要度をファジィ測度で表し、代替案の属性ごとの評価値をショケ積分で総合化した結果を、その代替案の総合評価値とする。また、ファジィ測度 μ が事象の生起に関する主観的な確からしさを測っているとき、すなわち μ が非加法的主観確率であるとき、ルベーグ積分が確率測度に関する期待値の算出に用いられるのと同様に、ショケ積分は非加法的確率 μ に関する期待値の算出に用いられる[15]。
　数学的観点からすれば、ファジィ測度に関する積分のなかで真に本質的なものは、基数モデルのChoquet積分と序数モデルの菅野積分ではないか、と考えられる[12]。

参考文献

菅野積分の進化

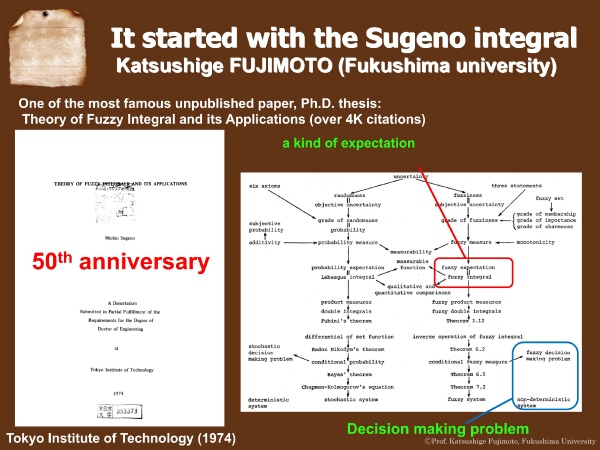
菅野先生の卓越した業績は、「ファジィ積分」から始まりました。 こちらはファジィ積分が初めて登場した文献です。
（1971年、情報処理学会システム制御シンポジウムでの口頭発表）

ファジィ積分の分野で、常に参照され引用されている文献といえば、菅野先生の博士論文「Theory of fuzzy integrals and its applications」です。被引用数は4000件以上あります。 この論文では主に、ファジィ積分による確率の一般化や意思決定問題を論じています。
なお、今年（2024年）は論文執筆から50周年にあたります。

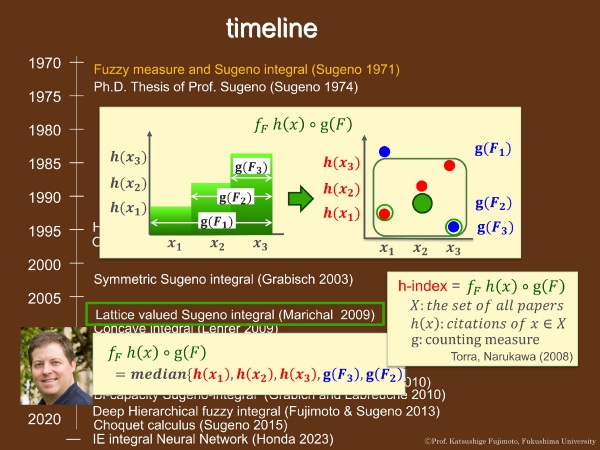
ここで、ファジィ積分の研究の歴史を振り返りましょう。
ファジィ測度と積分が提案されてから約20年後、ファジィ研究分野と経済学の分野において、ショケ積分が提案されました。 その後、ファジィ積分の様々な拡張概念や応用が提案されています。

下の画像の１つ目の図は、ファジィ測度 g を用いた関数 h の菅野積分を表します。 右側の赤の点は、 x₁ , x₂ , x₃ についての関数 h の値です。青の点は、各セグメントでファジィ測度 g により測定される値です。 ここで x₁ , x₂ , x₃ のそれぞれで赤と青を比較して小さいほうを選び、それらの最大（緑の点）を選ぶとちょうど菅野積分になります。
（注：この図では緑の点の後ろに青の点が隠れています）

Marichal（2009年）は、菅野積分はメディアン（中央値）を導出することを証明しました。
（図の右側で四角で囲まれた中の５つの点の中央）
また、Torraと成川（2008年）により、h-indexは菅野積分であることが証明されています。
（Xは全論文の集合、hは各論文の被引用数、gは計数測度としてのファジィ測度）

ショケ積分は次の図のように求められます。

その後、ファジィ積分を一般化する様々な拡張概念が提案されています。
たとえば、正負の値をとる関数hのファジィ積分（下の画像の１つ目の矢印）、正・負の領域でそれぞれ異なるファジィ測度を用いるもの（２つ目の矢印）、関数hの正・負の領域の統合に用いる測度（３つ目の矢印）、関数hの領域XをXのべき集合へ拡張したもの（４つ目の矢印） などがあります。

次にファジィ積分の応用を紹介します。
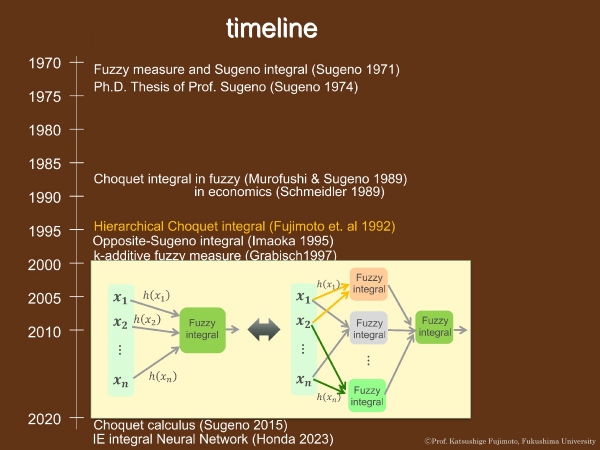
[Hierarchical Choquet integral (Fujimoto, et al. 1992)]
この研究では、通常のChoquet積分モデルと等価な階層的Choquet積分モデルを提案し、階層化のための必要十分条件を示しています。

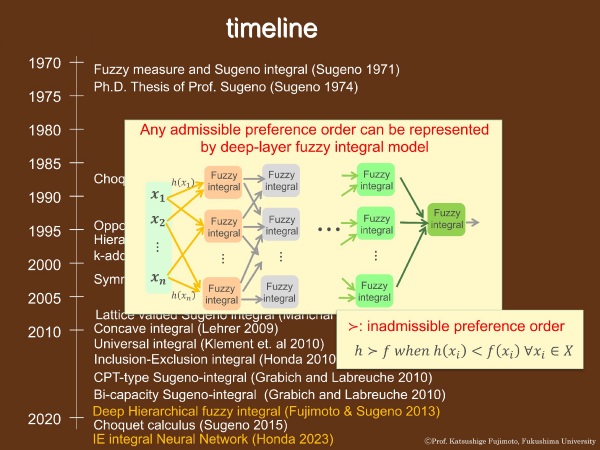
ここからは、菅野先生が70歳を過ぎてからの研究です。藤本、菅野（2013年）は、Admissibleな選好関係はすべて、階層型菅野積分によって表現できることを証明しました。
この研究は現在、九州工業大学の本田あおい教授によって継続されています。

菅野先生は晩年、ショケ微積分の研究に没頭していました。70歳を過ぎてから作成した研究ノートは100冊以上に及びます。
この研究は現在、スウェーデン Umeå大学のVicenç Torra教授と玉川大学の成川康男教授によって継続されています。

ショケ微積分学

著作・口頭発表