研究Studies

区分的多重線形モデル（Piecewise Multi-Linear (PML) Models)

非線形システムの構造，特性ごとに様々な非線形システム解析，設計手法が提案されています．本稿で取り扱う区分的システムは汎用的な非線形システムの解析，制御系設計の実現を目指しています．高木・菅野ファジィモデルも非線形システムに対する汎用的な非線形システム解析，設計手法の一つであると言えます．本稿の区分的システムは状態空間を矩形領域に分割してモデリングを行うため，モデル構造が単純でモデル化が容易である点が特徴です．
　本稿の区分的モデルとして，非線形性を有するモデルを用いています．モデル名称として，区分的パラメトリック近似モデル，区分的近似非線形モデル，タイプⅡファジイモデル，区分的非線形モデル，区分的双線形モデル，区分的マルチアファインモデル，区分的多重線形モデルなどを用いられています．本稿で扱う区分モデルの一般的な表現として，菅野先生が最終的に命名された区分的多重線形（Piecewise Multi-Linear：PML）モデルを用います．

非線形システムのモデルとして菅野先生が提案したPMLモデル [1] を用いています．このモデルの特徴として，
1) 後件部がシングルトンのファジィ If-then ルールとして表現できる
2) 状態空間を矩形領域に分割した区分モデルとして構築される
3) 非線形システムの Universal approximator としてモデル化できる
4) 区分領域の境界上で連続でモデルがパラメトリックに表現できる
点が挙げられます．このモデルは状態空間表現に加えて，ファジィ If-then ルールとしても記述できる点が特徴です．

ファジィ If-then ルールには多様な表現が存在しますが，以下の3種類のファジィモデルを記します．
・タイプⅠファジィシステム
\(\quad \rm{Rule\ }\it{i}\rm{\,:\ If\ }\it{x_1}\rm{\ is\ }\it{G_{i1}}\rm{\ and\ …\ and\ }\it{x_n}\rm{\ is\ }\it{G_{in}}\rm{\,,\ then\ }\it{y}\rm{\ is\ }\it{H_i\,.}\) ・タイプⅡファジィシステム
\(\quad \rm{Rule\ }\it{i}\rm{\,:\ If\ }\it{x_1}\rm{\ is\ }\it{G_{i1}}\rm{\ and\ …\ and\ }\it{x_n}\rm{\ is\ }\it{G_{in}}\rm{\,,\ then\ }\it{y}\rm{\ is\ }\it{f_i\,.}\) ・タイプⅢファジィシステム
\(\quad \rm{Rule\ }\it{i}\rm{\,:\ If\ }\it{x_1}\rm{\ is\ }\it{G_{i1}}\rm{\ and\ …\ and\ }\it{x_n}\rm{\ is\ }\it{G_{in}}\rm{\,,\ then\ }\it{y}\rm{\ is\ }\it{f_i}\rm{\,(}\it{x_1 , . . . , x_n}\rm{) .}\) ただし状態\(\ x \in R^{n}\,\)，ルール数は\(\ i=1, . . . , n\ \)です．\(\,G_i\ \),\(\ H_i\ \)はファジィ集合であり，\(\,f_i\ \)はシングルトン，\(\,f_i\,(x_1 , . . . , x_n)\ \)は通常，線形関数が用いられます．
　タイプⅠファジィシステムは Mamdani による蒸気エンジンの制御等に使用されており，後件部がファジィ集合のため確定値に変換する操作である非ファジィ化が必要です．PMLモデルはタイプⅡのファジィモデルに該当します．タイプⅡファジィシステムは後件部がシングルトンで表現されているため，非ファジィ化過程が省略できます．タイプⅢのファジィシステムは高木・菅野ファジィモデル [2,3] で用いられており，他のファジィシステムに比べてルール数が少なく，非線形関数を厳密に表現できます．

タイプⅡファジィシステムで表現されたPMLモデルとタイプⅢファジィシステムで表現された高木・菅野ファジィモデルは以下のように状態空間表現で表現することができます．ただし簡略化のため2次元システムを示し，連続時間，離散時間システムをまとめて\(\ x^{*}\ \)として示します．ただし\(\ d(i,j) = (d_1(i),d_2(j))^{T}\ \)です．

PMLモデル
高木・菅野ファジィモデル

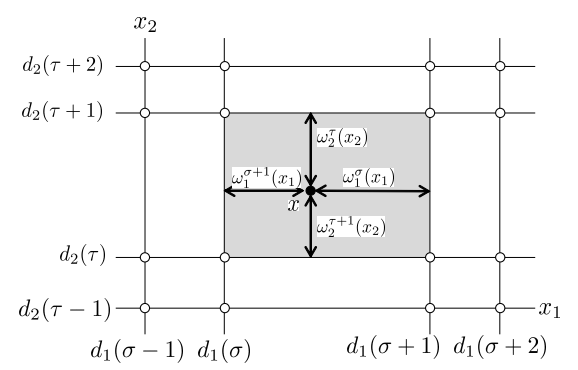
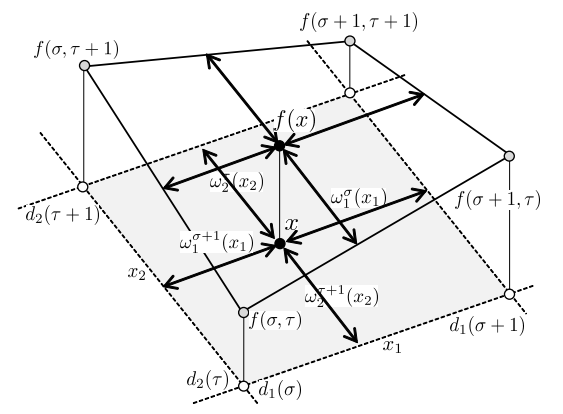
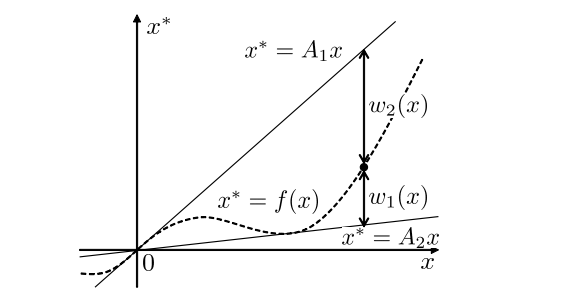
PMLモデルでは状態空間を矩形の領域に分割しています．また三角型のメンバーシップ関数 ω(x) を用い，それぞれの領域の端点の値の凸結合としてモデルを構成しています(図1, 2)．高木・菅野ファジィモデル [3] では，非線形システムをr 個の線形システムで挟み込み，適合度をメンバーシップ関数 w_i(x) で表現しています(図3)．

タイプⅠファジィシステムによる制御系の解析は一般的に困難です．高木・菅野ファジイモデルでは，非線形システムをモデル化誤差の観点から厳密に表現可能であり，十分条件ではありますが線形制御理論が適用できるため，多種多様な制御性能を考慮できます．対してPMLモデルは，区分的パラメトリック近似によるものであり，弱い非線形性を有するPMLモデルで構成しています．状態空間を矩形領域で分割して端点値のみ用いるためモデル化が容易で，区分領域数や分割点によってモデル化精度を調整できる点，また隣り合う区分領域が連続であるため微分可能であることが特徴です．

論文 [1] では，シングルトン後件部を有するファジィルールによって表現されたファジィシステムの安定性の問題を扱っています．ファジィシステムの2つの正準形式として，パラメトリック表現と状態空間表現を示しています．この論文ではシングルトンの後件部を持つファジィシステムは，区分的ポリトピック•アフィンシステムであることを示しています．さらに離散時間系と連続時間系の安定性定理を導出しています．
　論文 [4] では，ファジィ制御理論を確立するためにファジィ制御器の構造と同様の制御対象のファジィモデルを得ることが重要であるとしています．論文 [1] で提案されたタイプⅡファジィシステムの正準形式に対し，大域的な2次リアプノフ関数を用いて，安定性を満足する行列不等式で記述された必要十分条件を導出しています．

論文 [5] では，動的ファジィシステムの特殊なクラスとして，区分的双線形モデルとリカレントファジィシステムについて論じています．その安定性は区分的2次リアプノフ関数の近似に基づきLMIで定式化していますが，高次元のシステムへの適用には安定条件の保守性を回避する必要がある場合があると論じています．
　論文 [6] では，区分的マルチアファインシステムの漸近安定性を考慮する計算手法を提案しています．シングルトン後件部を持つファジィシステムを用いて非線形システムに対し，任意の精度で任意の滑らかな非線形システムとして近似しています．区分的リアプノフ関数を構成することで，LMI制約を持つ凸最適化問題として安定条件を表現しています．

論文 [7] では，Mamdani-like ファジィシステムと呼ばれる，シングルトン後件部を持つ離散時間ファジィシステムの安定性を考慮しています．このクラスのファジィシステムに特有なパラメトリック表現を用いて保守性を軽減した安定性条件を導出しています．また Mamdani-like ファジィシステムの安定条件をLMIで表現し，ファジィシステムの安定性を判別しています．

論文 [8,9] では，区分的2次リアプノフ関数による非線形システムの安定化条件を導出しています．安定条件は必要十分条件の行列不等式として導出しており，安定性を考慮する際の保守性を軽減しています．安定化条件は領域ごとにリアプノフ関数を構成できる事から領域ごとに制御性能を考慮することが可能です．安定化条件はBMIでかつ設計変数が多いため，一般的な解法である分枝限定法や主緩和双対法では変数の数が多い制御問題を実時間内で解くことは困難です．そのため区分的近似システム，区分的リアプノフ関数の特性を考慮したBMI問題の解法アルゴリズムを提案しています．

論文 [10] では，シングルトン後件部を持つファジィ If-then ルールで近似された連続時間非線形制御系のモデリングと安定化を扱っています．近似されたモデルは区分的双線形であり，非線形関数の区分的双線形近似の最適化と入出力フィードバック線形化 [11] による安定化制御器の設計手法を提案しています．
　論文 [12] では，入出力フィードバック線形化 [13] に基づく離散時間PMLシステムと区分的制御器を提案しています．入出カフィードバック線形化を用いて，各PMLモデルを Brunovsky 正準形式として知られる線形システムに変換し，区分的システム全体の安定化を実現しています．

PMLシステムに対して以下の制御性能を考慮した制御器を提案しています．

厳密なフィードバック線形化 [11] によるPMLシステムの安定化制御器設計手法 [10]，全状態フィードバック線形化による区分的制御器の設計 [14]，入出力安定化によるルックアップテーブル制御器の設計 15] を提案しています．
　PMLシステムは非線形近似モデルであるため，パラメータの不確かさを有するシステムに対してロバスト安定性を保証する制御器の設計 [16,17]，1入力1出力 (SISO) のシステムだけではなく，多入力多出力のシステムであるMIMOシステムの安定化 [18] を実現しています．また非線形サーボ系の制御器の設計 [19]，全状態オブザーバの設計 [20,21] と最小次元オブザーバの設計 [20] を実現しています．
　動的フィードバック線形化を用いた追従制御として，クアッドロータ制御手法の開発 [22]，ノン・ホロノミックシステムに対する制御器設計 [23-25] を提案しています．
　矩形領域でモデリングを行うPMLシステムとモデルの構造的に親和性が高く，実応用で広く使われているルックアップテーブル制御器の設計手法として，パラメータの不確かさを持つ非線形システムに対するロバストルックアップテーブル制御器の開発 [26]，入力値制限を考慮したルックアップテーブル制御器の開発 [27] を行っています．

離散時間非線形システムに対するフィードバック線形化手法 [13] による安定化制御器の設計手法の開発 [12]，入出力線形化手法による安定化 [28]，離散時間MIMOシステムに対する出力追従制御手法の開発 [29]，非線形追従制御手法の開発 [30,31] を行っています．

ロボットアーム等の運動機構はフィードバック制御では時間遅れが発生し，高速かつ正確な制御は困難です．これらの運動ではフィードフォワード制御が重要な役割を担っており，論文 [32] では小脳が腕の物理モデルを学習し腕の運動制御はフィードフォワード制御が担っていると述べ，上記の制御系はフィードバック誤差学習によって対象システムの逆モデルを学習し，フィードフォワード制御を実現すると考えています．論文 [33-35] では，フィードバック誤差学習によるフィードフォワード制御器をPMLモデルを用いて，ルックアップテーブルとして表現しています．

この論文 [36] では，数値データを用いPMLシステムを構築するモデリングアルゴリズムを提案しています．このPMLシステムはファジィ if-then ルールとしても表現できることを利用し，簡略ファジィ推論を用いたモデリングアルゴリズム [37] に基づき区分モデルの端点値を決定しています．端点値と領域分割点の導出は非線形計画問題であるため，大域的な最適解を導出することは困難です．区分モデルの端点値と領域分割点の導出については簡略ファジィ推論の手法とスプライン関数最小化アルゴリズムを組み合わせてモデル化を実現するアルゴリズムを提案しています．

---

参考文献